
- Matemática no Marketing: A estatística é essencial para decifrar padrões e prever vendas com base em dados de campanhas.
- Regressão Linear Simples: Utiliza uma variável independente (como gastos em marketing) para prever uma variável dependente (vendas), representada por uma linha reta.
- Regressão Linear Múltipla: Considera múltiplos fatores, como preço e economia, para criar previsões mais precisas e robustas, capturando a complexidade do mercado.
Matemática como Linguagem do Marketing
Desde os tempos antigos, a matemática é vista como a linguagem do universo, capaz de descrever desde o movimento dos planetas até o crescimento das plantas. No contexto do marketing, a matemática nos permite decifrar padrões ocultos nas quantidades infindáveis de dados gerados pelas campanhas publicitárias, principalmente por meio da estatística. A seguir, explicamos uma das principais ferramentas numéricas que estruturam uma análise de Marketing Mix Modeling, a Regressão.
- Leia também: Introdução ao Marketing Mix Modeling (MMM)
Regressão Linear: A Simplicidade da Reta
O MMM é tanto uma análise quanto uma previsão. No fim das contas, o que estamos querendo fazer é estimar valores que inicialmente não poderiam ser previstos. Na estatística, a ferramenta mais simples e didática para fazer esse trabalho é a regressão linear. A regressão é uma equação para se estimar o valor esperado de uma variável e, dados os valores de algumas outras variáveis x.
Vamos, a título de exemplo, criar um modelo muito elementar, onde utilizamos dados de gastos em marketing para prever vendas futuras com uma regressão linear simples.
Exemplo: Uma relação entre investimento e vendas
Usando dados fictícios de 12 meses podemos tentar prever as vendas para os próximos 3 meses com base nos gastos em marketing.
E agora vamos supor os seguintes gastos em marketing para os próximos 3 meses:
Finalmente, usamos a regressão linear para prever as vendas para os meses 13, 14 e 15
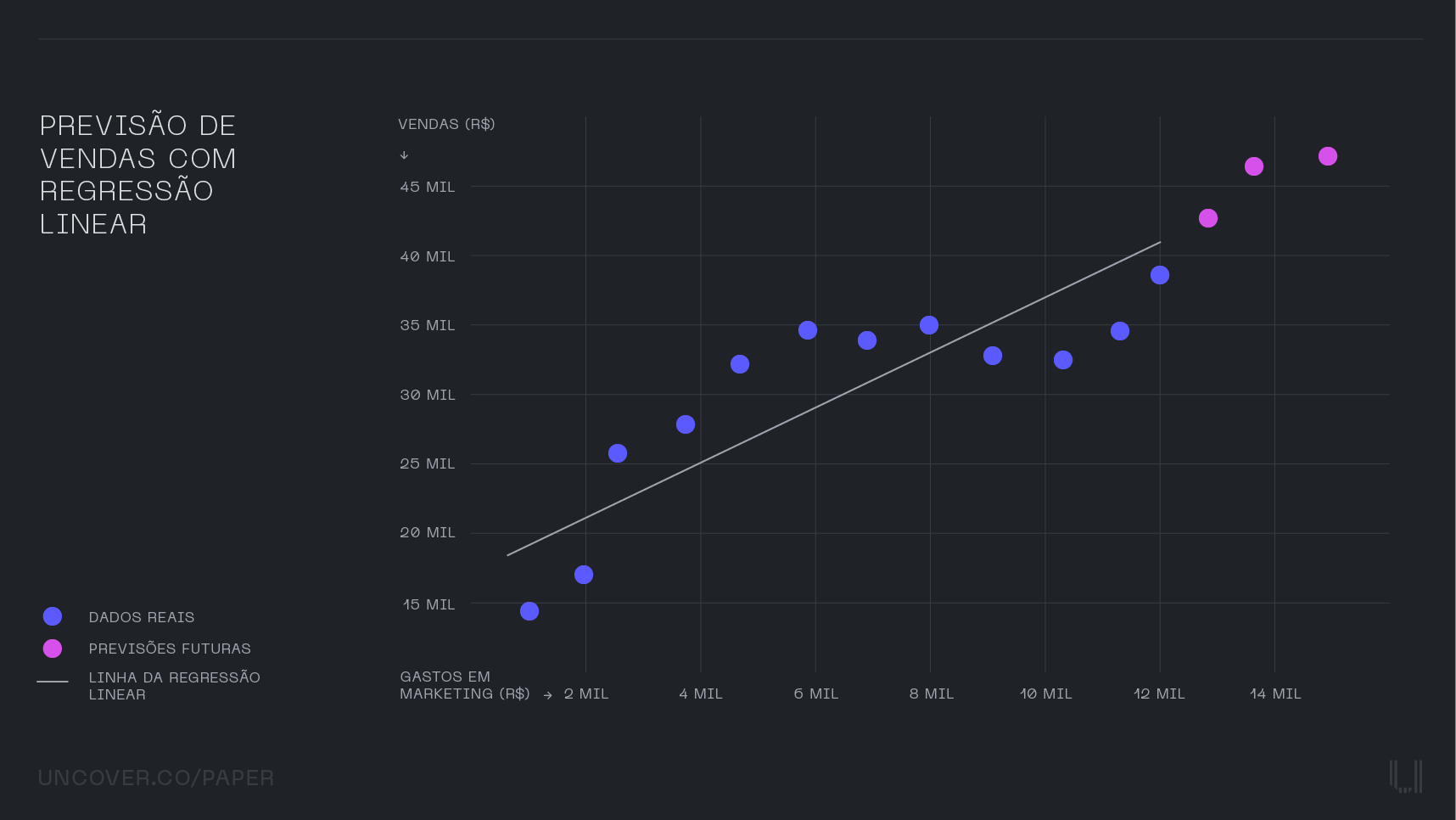
Pontos Azuis: Representam os dados reais de gastos em marketing e vendas dos 12 meses iniciais.
Linha: Representa a linha de regressão linear ajustada aos dados.
Pontos Roxos: Representam as previsões de vendas para os meses 13, 14 e 15 com base nos gastos em marketing previstos.
A regressão linear simples segue a fórmula:
Y = β0 + β1X
Onde:
Y é o valor das vendas previstas
β0 é a constante
β1 é o coeficiente de inclinação
X é a variável independente (gastos em marketing)
Você pode experimentar fazer uma regressão simples com os seus dados de marketing e vendas, usando o comando PREVISÃO.LINEAR no Excel.
Incorporando Múltiplos Fatores
Embora a regressão linear simples seja útil para prever uma variável dependente (como vendas) com base em uma única variável independente (como gastos em marketing), na realidade, no MMM calculamos a influência de múltiplos fatores. Para capturar essa complexidade, utilizamos a regressão linear múltipla.
Na regressão linear múltipla, consideramos várias variáveis independentes (por exemplo, gastos em marketing, preço do produto, condições econômicas) para prever a variável dependente (vendas). A fórmula da regressão linear múltipla é uma extensão da fórmula da regressão linear simples e pode ser escrita assim:
Y = β0 + β1X1 + β2X2 + β3X3 + ϵ
Onde:
Y são as vendas previstas
X1são os gastos em marketing
X2 é o preço do produto
X3 é a taxa de crescimento econômico
β0, β1, β2, β3são os coeficientes do modeloϵ é o erro
Ao usar a regressão linear múltipla, podemos prever as vendas levando em consideração não apenas os gastos em marketing, mas também outros fatores que podem influenciar o resultado. Isso torna as previsões mais robustas e precisas, refletindo melhor a realidade complexa do mercado.
Exemplo Prático de Regressão Linear Múltipla:
Suponha que, além dos gastos em marketing, também tenhamos dados sobre o preço do produto e a taxa de crescimento econômico nos últimos 12 meses. Podemos usar esses três fatores para criar um modelo de regressão linear múltipla que preveja as vendas para os próximos 3 meses. A fórmula ajustada seria:
Y = β0 + β1(Gastos em Marketing) + β2(Preço do Produto) + β3(Crescimento Econômico) + ϵ
Vamos então criar mais um conjunto de dados fictícios para as variáveis mencionadas, considerando três variáveis independentes (gastos em marketing, preço do produto e taxa de crescimento econômico) para prever uma variável dependente (vendas).
Gastos em Marketing (X1): Em milhões de reais
Preço do Produto (X2): Em reais
Taxa de Crescimento Econômico (X3): Em porcentagem
Vendas (Y): Em milhões de unidades
Como os Coeficientes da fórmula são Calculados?
Os coeficientes são calculados usando o método dos mínimos quadrados. Esse método ajusta a linha que minimiza a soma dos quadrados das diferenças entre os valores reais e os valores previstos pelo modelo. O cálculo dos coeficientes envolve os seguintes passos:
Organize os dados em uma matriz.
Multiplicar a matriz de dados por sua transposição.
Calcular a inversão da matriz resultante.
Multiplicar o resultado pelo vetor de valores observados (vendas).
A função de regressão linear do Excel faz esse cálculo automaticamente. Ver PROJ.LIN
Coeficientes calculados
Com base nos cálculos, os coeficientes da equação de regressão linear múltipla são:
β0 = 28.04
β1 = 4,58 (para Gastos em Marketing)
β2= -0,12 (para Preço do Produto)
β3 = 1,64 (para Taxa de Crescimento Econômico)
Assim, a equação de regressão para prever as vendas (Y) é:
Y = 28,04 + 4,58×X1 -0,12×X2 + 1,64×X3
Previsão para os Próximos 3 Meses
Agora, vamos prever as vendas para os próximos 3 meses, supondo que temos as seguintes condições futuras:
Resultados das Previsões
As previsões para as vendas nos próximos 3 meses são:
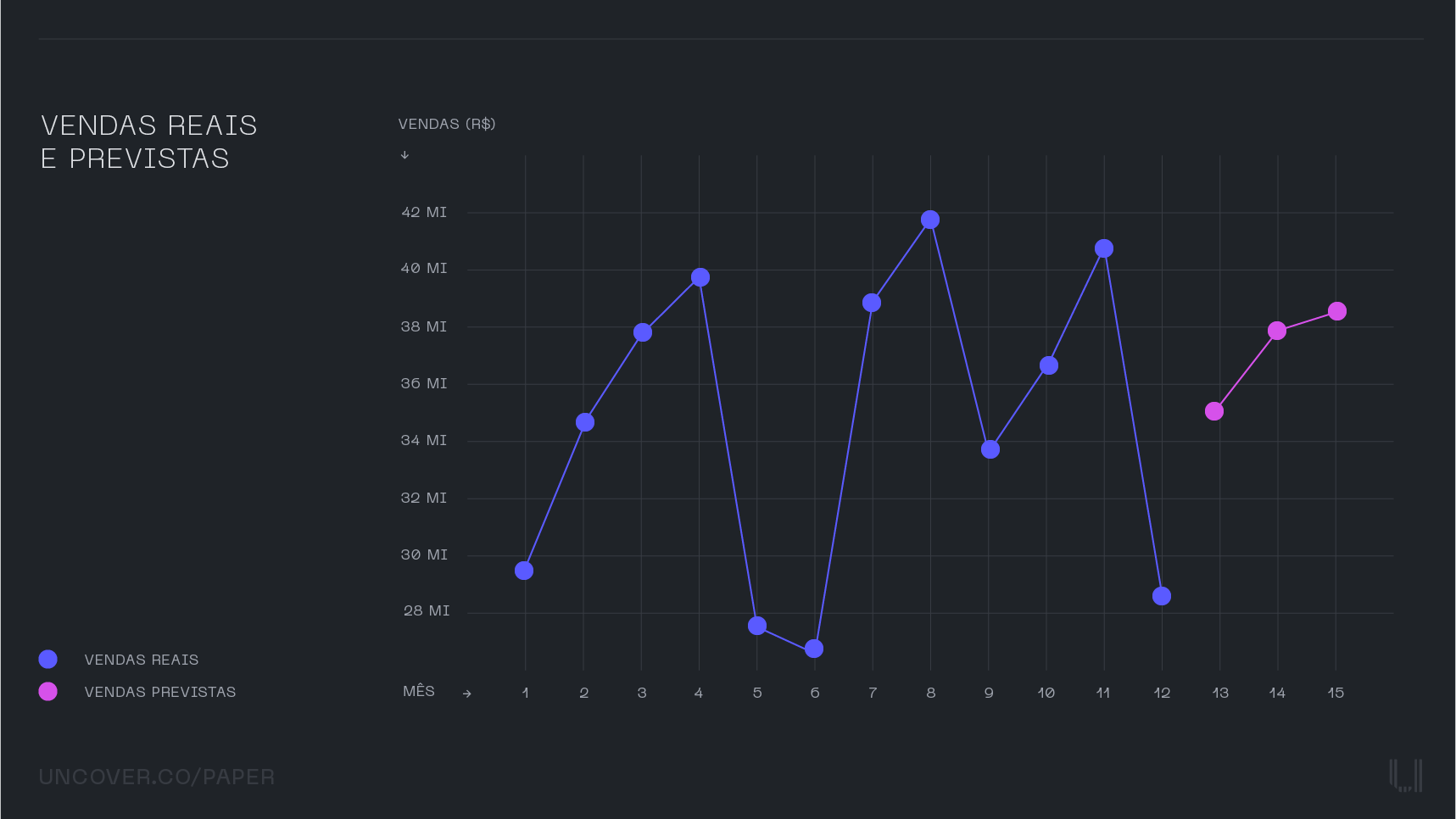
Mês 13: 35,41 milhões de unidades
Mês 14: 37,93 milhões de unidades
Mês 15: 38,44 milhões de unidades
Incorporando o Erro
O termo de erro ϵ representa a diferença entre o valor real observado das vendas Y e o valor previsto pelo modelo de regressão. O erro captura as variações nos dados que não são explicadas pelas variáveis independentes incluídas no modelo.
ϵ = Y(real) - Y
O erro pode ser causado por:
Fatores não incluídos no modelo: Como o modelo só leva em conta os gastos em marketing, preço do produto e taxa de crescimento econômico, qualquer outro fator que influencie as vendas (como sazonalidade, mudanças de comportamento do consumidor, etc.) será capturado no erro.
Ruído aleatório: Pequenas variações que ocorrem naturalmente nos dados e não seguem um padrão específico.
Previsão e Cálculo do Erro
Suponha que para o mês 13, os valores das variáveis sejam:
Gastos em Marketing (X1) = 3,2
Preço do Produto (X2) = 101
Taxa de Crescimento Econômico (X3) = 2,9
Usando a equação, a previsão seria:
Y13 = 25+3,5(3,2) - 0,2(101) +1,8(2,9) = 34,46 unidades
Se as vendas reais no mês 13 foram 36 unidades, o erro seria:
ϵ13 = Yreal - Y = 36 - 34,46 = 1,54 unidades
Conclusão
O erro ϵ é uma parte fundamental da análise de regressão, pois representa as variações que o modelo não conseguiu capturar. Ele nos ajuda a entender a precisão do modelo e a identificar áreas onde ele pode ser melhorado. Ao analisar os erros de forma sistemática, a empresa pode ajustar suas estratégias e melhorar suas previsões futuras.
